TEST FOR THE LAST YEAR OF SECONDARY EDUCATION (18YEARS
OLD) FOR ALL THE STUDENTS
SATURDAY 3 - 6 - 2000
PAGES: 5
ΑΠΟΛΥΤΗΡΙΕΣ
ΕΞΕΤΑΣΕΙΣ Γ΄
ΤΑΞΗΣ
ΕΝΙΑΙΟΥ
ΛΥΚΕΙΟΥ
ΣΑΒΒΑΤΟ
3 ΙΟΥΝΙΟΥ 2000
ΕΞΕΤΑΖΟΜΕΝΟ
ΜΑΘΗΜΑ ΓΕΝΙΚΗΣ
ΠΑΙΔΕΙΑΣ:
ΜΑΘΗΜΑΤΙΚΑ ΚΑΙ
ΣΤΟΙΧΕΙΑ ΣΤΑΤΙΣΤΙΚΗΣ
ΣΥΝΟΛΟ
ΣΕΛΙΔΩΝ: ΠΕΝΤΕ (5)
ΘΕΜΑ
1ο
Α. α) Δίνεται
η συνάρτηση
F(x)=f(x)+g(x). Αν οι
συναρτήσεις f, g
είναι
παραγωγίσιμες,
να αποδείξετε
ότι: F΄(x)=f΄(x)+g΄(x).
Μονάδες
8
β) Να
γράψετε στο
τετράδιό σας τις
παραγώγους των
παρακάτω
συναρτήσεων:
cf(x), f(x)g(x), 
όπου
c
πραγματική
σταθερά.
Μονάδες
4,5
Β. α) Να
γράψετε στο
τετράδιό σας
τα γράμματα
της στήλης Α
και δίπλα τον
αριθμό της
στήλης Β που
αντιστοιχεί
στη σωστή
απάντηση.
Στήλη Α
συνάρτηση |
Στήλη
Β πρώτη
παράγωγος |
|
α.
x2+3 |
1. 1-ημx |
|
β.
x+συνx |
2. 3x2-8x |
|
γ.
xημx |
3. 2x+3 |
|
δ.
x3-4x2 |
4. ημx-xσυνx |
|
|
5.
2x |
|
|
6.
3x2-4x |
|
|
7.
ημx+xσυνx |
Μονάδες
8
β) Να
γράψετε στο
τετράδιό σας
το γράμμα που
αντιστοιχεί
στη σωστή
απάντηση.
Η πρώτη
παράγωγος της
συνάρτησης
 είναι:
είναι:
Α:![]() , B:
, B:  , Γ:
, Γ: 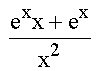 ,
,
Δ:  , Ε:
, Ε: 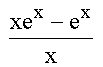
![]() Μονάδες 4,5
Μονάδες 4,5
ΘΕΜΑ
2ο
A.
Να γράψετε
στο τετράδιό
σας τον πίνακα
των τιμών της
μεταβλητής Χ σωστά
συμπληρωμένο.
|
Τιμές Μεταβλητής |
Συχνό-τητα |
Σχετική Συχνό-τητα |
Σχετική Συχνό-τητα |
Αθροιστική Συχνότητα |
|
|
|
|
|
|
|
fi% |
|
|
|
|
|
1 |
10 |
|
|
|
10 |
1 |
10 |
|
2 |
|
|
|
35 |
|
4 |
|
|
3 |
|
|
|
|
|
9 |
|
|
ΣΥΝΟΛΟ |
ν=50 |
1 |
100 |
|
|
|
|
Μονάδες
16
B. Να
υπολογίσετε τη
μέση τιμή και
τη διάμεσο.
Μονάδες
4
Γ. Να δείξετε
ότι η
διακύμανση
είναι s2=0,49.
Δίνεται
ότι: 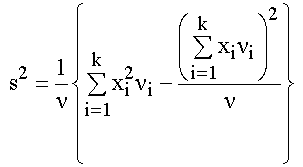
Μονάδες
5
ΘΕΜΑ
3ο
Από 120
μαθητές ενός
Λυκείου, 24
μαθητές
συμμετέχουν στο
διαγωνισμό
της Ελληνικής
Μαθηματικής
Εταιρείας, 20
μαθητές
συμμετέχουν
στο διαγωνισμό
της ΄Ενωσης Ελλήνων
Φυσικών και 12
μαθητές συμμετέχουν
και στους δύο
διαγωνισμούς.
Επιλέγουμε
τυχαία ένα
μαθητή. Ποια είναι
η
πιθανότητα ο
μαθητής:
Α. να
συμμετέχει σ’
έναν
τουλάχιστον
από τους δύο διαγωνισμούς;
Mονάδες
8
Β. να
συμμετέχει
μόνο σ’ έναν από
τους δύο
διαγωνισμούς;
Mονάδες
8
Γ. να μη συμμετέχει
σε κανέναν από
τους δύο
διαγωνισμούς;
Mονάδες
9
ΘΕΜΑ
4ο
Στα
σχολεία ενός
Δήμου
υπηρετούν
συνολικά 100 εκπαιδευτικοί.
Ο συνολικός
χρόνος
υπηρεσίας των
εκπαιδευτικών
δίνεται από
τον παρακάτω
πίνακα:
|
Χρόνια
υπηρεσίας [ -
) |
Σχετική
Συχνότητα fi% |
|
0-
5 |
10 |
|
5-10 |
15 |
|
10-15 |
12 |
|
15-20 |
15 |
|
20-25 |
18 |
|
25-30 |
18 |
|
30-35 |
12 |
Α.
Πόσοι
εκπαιδευτικοί
έχουν
τουλάχιστον 15
χρόνια υπηρεσίας;
Μονάδες
5
Β. Με
την προϋπόθεση
ότι κάθε
εκπαιδευτικός
θα συνταξιοδοτηθεί,
όταν
συμπληρώσει 35 χρόνια:
α) πόσοι
εκπαιδευτικοί
θα
συνταξιοδοτηθούν
μέσα στα
επόμενα 12,5
χρόνια; Να
δικαιολογήσετε
την απάντησή
σας.
Μονάδες
10
β) πόσοι
συνολικά
εκπαιδευτικοί
πρέπει να
προσληφθούν
μέσα στα
επόμενα πέντε
χρόνια, ώστε ο
αριθμός των
εκπαιδευτικών
που υπηρετούν
στα σχολεία
του Δήμου να
παραμένει ο
ίδιος; Να
δικαιολογήσετε
την απάντησή
σας.
Μονάδες
10