PRUEBAS DE ACCESO A LA UNIVERSIDAD CONVOCATORIA: JUNIO CURSO: 1999-2000

- El alumno elegirá una de las dos opciones (A o B)

- Contestará a las cuatro cuestiones de la opción elegida

- Puntuación de cada cuestión: máximo 10 puntos

- Se puede utilizar calculadora.

- Se valorará la expresión escrita de los pasos y razonamientos realizados.

OPCIÓN A

CUESTIÓN 1.-

Dada la función

f(x) = 5+2 sen x si x 0

f(x)= -x² +ax +b si x > 0

a) ¿Para que valores de los parámetros a y b es continua la función f(x)?

b) Determinar a y b para que f(x) sea derivable en x = 0

CUESTIÓN 2.-

Un jardinero dispone de 160 metros de alambre que va a utilizar para cercar una zona rectangular y dividirla en tres partes, colocando las alambradas de las divisiones paralelas a uno de los lados del rectángulo. ¿Qué dimensiones debe tener la zona cercada para que el área sea la mayor posible?

CUESTIÓN 3.-

Se consideran las matrices

A = 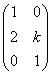y B =

a) Discutir, en función de los valores que pueda tomar k, si la matriz A x B tiene inversa.

b) Discutir, en función de los valores de k, si la matriz B x A tiene inversa.

CUESTIÓN 4.-

Discutir, según los valores de k, la posición relativa de los planos

a : 2x +3y - 4z = 1

b : 4x +6y -kz = 2

c : x + y + kz = 10

OPCIÓN B

CUESTIÓN 1.-

El precio (en miles de pesetas) de un determinado modelo de radiocasette, que se ha vendido durante 8 años, ha variado con el tiempo de acuerdo con la siguiente regla: Los dos primeros años, el precio fue p(t) = 4(t² + 1), y los últimos 6 años fue p(t) = - 2´5 t + 25

a) Representar gráficamente la función precio

b) Decidir acerca de si es continua o no.

c) Calcular cuál fue el precio máximo alcanzado por el aparato. Explicar por qué no se pudo calcular mediante derivadas.

CUESTIÓN 2.-

En la figura aparece una curva que representa a una función polinómica de grado 2. Los puntos de intersección de la curva con el eje OX son el (1,0) y el (3,0). Además, el área limitada por la curva y los dos ejes coordenados vale 4/3. Hallar la expresión de la función polinómica.

CUESTIÓN 3.-

Dada la matriz

A=

a) Calcular 3A x A´ - 2I (I = matriz unidad de orden 2)

b) Resolver la siguiente igualdad matricial A . X =

CUESTIÓN 4.-

Se dan dos rectas definidas por las ecuaciones siguientes:

r : s :

a) Investigar si son paralelas.

b) En caso afirmativo, hallar la ecuación del plano que las contiene.