ACCUEIL

COMENIUS  PROJECT

e-teaching

Retour accueil

Correction Brevet Juin 2006 Nancy-Metz

D’après :

http://www.ilemaths.net/maths_3-sujet-brevet-06-01-correction.php#correction

Partie A

1. Montrons que le volume de cette piscine est 91 m³ :

le volume de cette piscine est 91 m³.

2. a) Calcul du nombre de m³ d’eau restant dans la piscine au bout de 5 heures :
Au bout de 5 heures, il y a eu 5 × 5 = 25 m³ d’eau enlevés de la piscine.
Il reste donc 91 – 25 = 66 m³ d’eau dans la piscine.

b) Représentons graphiquement la fonction dans le repère :

La fonction est une fonction affine, sa représentation graphique est une droite ne passant pas par l'origine du repère.

Détermination de deux points de la droite :
f(5)=66 (calculs effectués à la question précédente)

Et f(16)=91-5x16 = 91-80 =11

La droite passe par les points de coordonnées (5 ; 66) et (16 ; 11).

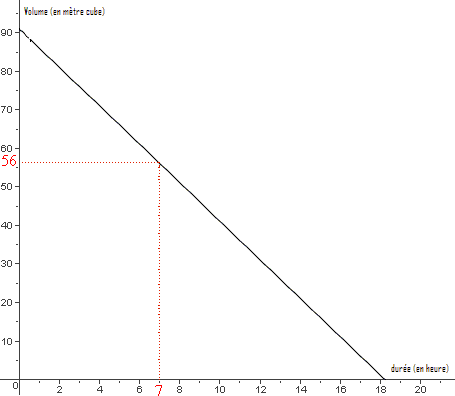
c) Déterminer le nombre d’heures nécessaires pour qu’il ne reste que 56 m³ d’eau dans cette piscine :

Graphiquement, le nombre d’heures nécessaires pour qu’il ne reste que 56 m³ d’eau dans cette piscine est de 7 heures (cf pointilles rouges sur le graphique).

d) Graphiquement, le nombre d’heures nécessaires pour vider complètement la piscine est de 18,2 heures

(c'est l'abscisse du point d'intersection de la droite représentant la fonction et l'axe des abscisses).

e) Retrouver ce dernier résultat par le calcul :

Pour déterminer par le calcul le nombre d'heures nécessaires pour vider complètement la piscine, nous devons résoudre l’équation suivante : f ( x ) = 0

91 – 5x = 0

5x = 91

x = 18,2
.
Nous avons donc retrouvé le résultat de la question précédente.
Et : 0,2 h = 0,2 × 60 min = 12 min, donc il faut 18 h 12 min pour vider complètement la piscine.

Partie B

1. Calcul des distances IJ et JK :

AE = 5 m, donc IJ = AE + 1,25 × 2 = 5 + 2,5 = 7,5
D'où : IJ = 7,5 m = 750 cm

AB = 14 m = EF, donc JK = EF + 2 × 1,25 = 14 + 2,5 = 16,5
D'où : JK = 16,5 m = 1 650 cm

La longueur a d'un panneau est un entier qui divise IJ et JK. Le nombre a est donc un diviseur de 750 et 1 650.

De plus, on veut que le nombre a soit le plus grand possible, c'est donc le plus grand commun diviseur de 750 et 1 650, donc a = PGCD(1 650 ; 750).

2. Calcul de la valeur de a :
Détermination du PGCD de 750 et 1 650 :
. -Par la méthode des soustractions successives :
PGCD(1 650 ; 750) = PGCD(900 ; 750) car 1 650 - 750 = 900
PGCD(900 ; 750) = PGCD(750 ; 150) car 900 - 750 = 150
PGCD(750 ; 150) = PGCD(600 ; 150) car 750 - 150 = 600
PGCD(600 ; 150) = PGCD(450 ; 150) car 600 - 150 = 450
PGCD(450 ; 150) = PGCD(300 ; 150) car 450 - 150 = 300
PGCD(300 ; 150) = PGCD(150 ; 150) car 300 - 150 = 150
PGCD(150 ; 150) = 150
D'où : PGCD(1 650 ; 750) = a = 150

. -En utilisant l'algorithme d'Euclide :
1 650 = 750 × 2 + 150
750 = 150 × 5 + 0
Le dernier reste non nul est 150, donc PGCD(1 650 ; 750) = a = 150
La longueur d'un panneau est de 150 cm.

3 Détermination du nombre de panneaux nécessaires pour clôturer la piscine :
On a 750 = 150 × 5, il faut donc 5 panneaux pour clôturer la longueur IJ.
1 650 = 150 × 11, il faut donc 11 panneaux pour clôturer la longueur JK.
D'où : il faut (11 + 5) × 2 = 16 × 2 = 32 panneaux pour former la clôture de la piscine.

Retour accueil