|
e-teaching |
e-teaching exercise french "BREVET"
| BREVET 2006 JUIN Nancy-Metz format .doc |
| BREVET 2007 JUIN Amérique du nord géométrie de l' espacce format.ppt |
| BREVET 2007 JUIN Amérique du nord géométrie du plan - Transformations dans le plan format . ppt |
| BREVET 2006 SEPTEMBRE Nantes format . ppt |
e-teaching lesson
level : secondary school (14-15 years old student )
1 - Notion de Fonction format .ppt
............................................................................................................................................................................................................................
BREVET 2007 JUIN Amérique du nord géométrie de l'espace format .ppt
SABCD est une pyramide à base
rectangulaire ABCD, de hauteur [SA]. On donne SA = 15 cm, AB = 8 cm et BC = 11
cm.
1. Calculer
le volume
de la pyramide SABCD.
2. Démontrer
que SB = 17 cm.
3. On
note E le point de [SA] tel que SE = 12 cm et F le point de [SB] tel que SF =
13,6 cm.
Montrer que (EF) et (AB) sont parallèles.
4. On coupe cette pyramide par le plan passant par E et parallèle à la base de la pyramide.
La pyramide SEFGH, ainsi obtenue, est une réduction de la pyramide
SABCD.
a) Quel est le coefficient
de cette réduction ?
b) En déduire le volume
de la pyramide SEFGH en fonction de
.
BREVET 2007 JUIN Amérique du nord géométrie de l'espace format .ppt
...................................................................................................................ABCDHGFE est un cube d’arête 6 cm.
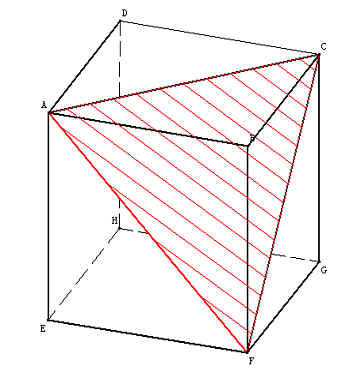
1-a) Construire, en vraie grandeur, le carré ABCD avec sa diagonale
[AC].
-b) Construire le triangle ACF en vraie grandeur.
2- Calculer AC
3- La pyramide ABFC a pour base ABF et pour hauteur le segment [BC ].
Calculer son volume
4- Est-il vrai que le volume de la pyramide ABFC est égal à 18% de
celui du cube ? Justifier
BREVET 2006 SEPTEMBRE Nantes format .ppt
......................................................................................................................
La piscine de Monsieur Dujardin a la forme d’un prisme droit dont la
base ABCD est un trapèze rectangle.
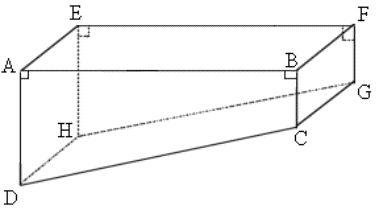
On donne : AB = 14
m, AE = 5 m, AD = 1,80 m, BC = 0,80 m.
Sur le schéma ci-dessus, les dimensions ne sont pas
respectées.
On rappelle les formules suivantes :
Aire d'un trapèze =
Volume d'un prisme = (Aire de la base) × hauteur.
Partie A
1. Montrer que le volume de cette piscine est 91 m3.
2. A la fin de l’été, M. Dujardin vide sa
piscine à l’aide d’une pompe dont le débit est 5 m3 par heure.
a) Calculer le nombre de m3
d’eau restant dans la piscine au bout de 5 heures.
b) On admet que le nombre
de m3 d’eau restant dans la piscine au bout de
heures est donné par la fonction
affine
définie par :
.
Sur la feuille de papier millimétré, construire un repère orthogonal tel que
:
en abscisse, 1 cm représente 1 heure,
en ordonnée, 1 cm représente 5 m3.
Représenter graphiquement la fonction
dans ce repère.
c) Par lecture graphique,
déterminer le nombre d’heures nécessaires pour qu’il ne reste que 56 m3
d’eau dans cette piscine.
d) Par lecture graphique,
déterminer le nombre d’heures nécessaires pour vider complètement la
piscine.
e) Retrouver ce dernier résultat
par le calcul.
Donner cette durée en
heures et minutes.
Partie B
M. Dujardin doit clôturer sa piscine, en laissant autour une distance
de 1,25 m comme le montre le schéma ci-dessous.
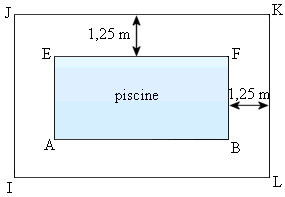
1. Calculer les distances IJ et JK
en cm.
2. Pour réaliser la clôture, il souhaite
utiliser un nombre entier de panneaux rectangulaires identiques, dont la
longueur a est un nombre entier de centimètres, le plus grand possible.
Expliquer pourquoi a est le PGCD de 750 et 1650.
3. Calculer la valeur de a, en indiquant la méthode
utilisée.
4. Combien faudra-t-il de panneaux pour clôturer
la piscine ?
BREVET
2006 JUIN Nancy-Metz format .doc
..........................................................................................................................................................................
BREVET 2007 Amérique du nord. Géométrie du plan - Transformations
Soit (O ; I , J) un repère orthononormé tel que OI = OJ = 1 cm.1. Sur votre copie,
construire ce repère et placer les points suivants :
A(0 ; 3) B(3 ; 0) E(-4 ;
3) F(-1 ; 2) G(-4 ; -1)
2. Tracer la droite (AB), puis le triangle EFG, noté par la suite T.
3. Constuire T1 l'image de T par la symétrie axiale (AB).
4. Constuire T2
l'image de T par la translation de vecteur .
5. Construire T3 l'image de T par la rotation de centre E et d'angle 100°, le sens étant le sens inverse des aiguilles d'une montre.
BREVET 2007 Amérique du nord. Géométrie du plan - Transformations
.........................................................................................................................................................................